Бадяева З.П. - Золотое сечение

Бадяева Зинаида Петровна

Золотое сечение

Опубликовано в журнале "Современная теософская мысль", 2016-2 (2)

«Главной целью всех исследований внешнего мира должно быть открытие рационального порядка и гармонии, которые Бог послал миру и открыл нам на языке математики»

Иоганн Кеплер

Елена Петровна Блаватская писала: «для философов каббалистов и философов герметиков всё в природе представляется в триедином аспекте: всё является множественным и троичным в единстве, и может быть символически представлено различными геометрическими фигурами».

Так, всем известный, древний философ Платон говорил: «Бог геометризирует». Так, куб символизировал царствование и земные основы, а золотое сечение считалось динамическим принципом, воплощающем в себе высшую мудрость. Храм, посвящённый земному правительству в основании его создания имели принципы золотого сечения. В более подробном докладе рассказывалось о том, что сакральная (тайная) геометрия основывается на 5 основных геометрических отношениях:

1) π;

2) √2;

3) √3;

4) √5;

5) или .

В этом докладе рассмотрим только пятое отношение. Это первое деление единого на множества.

Многие религиозные писания говорят, что в Начале был Единый Бог. Чтобы проявить себя, он реализовал принцип Золотого сечения. Золотое сечение знаменует собой изначальную красоту. Все последующие эманации, то есть деление Единого происходили и происходят на основе этого числа Ф.

В «Справочники по математике для средний школы» А.Г.Цыпкина даётся следующее определение:

«Число Ф называют отношением крайнего и среднего, так как оно определяется условием:

если то »

Известны и другие определения этого числа: божественная пропорция, золотое сечение. Само обозначение числа Ф (или φ=1/Ф) идёт от начальной буквы греческого скульптора Фидия, который активно применял этот принцип в своих творениях.

Этот коэффициент очень приблизительно выводится из равенства периметра квадрата и длины окружности.

Рассмотрим это значение.

Квадратура круга

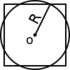
Пусть радиус круга R=1, а сторона квадрата равна х, тогда из равенства 2π*1=4х следует х=π/2≈1,57 очень ≈1,618. Но из квадратуры круга, когда площадь квадрата равна площади круга, следует πR²=х², то есть х=√π≈1,77. Легко увидеть, что 1,57<1,618<1,77. Можем заключить, что эти два значения: 1,57 и 1,77 — две границы числа Ф.

Леонардо Фибоначчи

Приведём пример ряда Фибоначчи (итальянский математик Леонардо из Пизы). Он в 1202 году исследовал возможность быстрого размножения кроликов в идеальных условиях: в начале первого месяца 1 пара; в конце этого первого месяца всё та же 1 пара; но в конце 2-го месяца уже две пары, затем три пары; потом 5 пар и т. д. То есть число пар кроликов в начале каждого месяца это:

1, 1, 2, 3, 5, 8, 13, …

Размножение кроликов

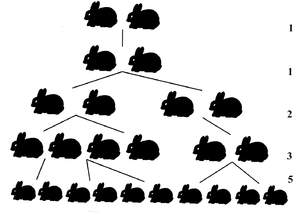
Математически такая последовательность может быть составлена или задана по возвратной формуле (в математике её называют рекуррентной): а₁=1, а₂=1, а_n+1=а_n+а_n-1. В этой последовательности отношение любой пары двух соседних чисел дают приближение к числу Ф=1,618. Достаточно проверить это:

действительно, чем больше номера n+1 и n, тем ближе отношения к 1,618.

Это универсальное отношение частей мироздания друг к другу, символически связывающее каждое новое поколение с его предками, сохраняя непрерывность отношений как средства восстановления его происхождения.

Рассмотрим другой пример золотого сечения — спираль или раковину. Как сказал Гёте: «спираль — геометрический символ жизни и духовного развития». Эти же числа Фибоначчи просматриваются и в спирали, которая легко строится по принципу золотых треугольников.

Спираль, построенная по золотому сечению

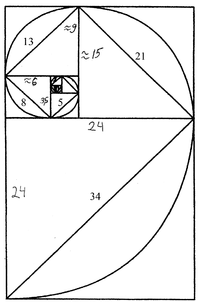
Все золотые треугольники имеют форму равнобедренного треугольника с гипотернузой равной числам из ряда Фибоначчи:

1, 1, 2, 3, 5, 8, 13, 21, 34, …

Спирали встречаем в природе:

Раковина улитки

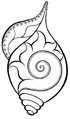
1) самоё распространённое её проявление в форме раковины улитки:

2) по спирали закручиваются усики вьющихся растений (пример: вьюнки; горох и т. п.)

3) по спирали происходит рост тканей в стволах деревьев

4) по спирали распределяются семечки в подсолнухах

5) сама молекула ДНК закручена в спираль.

Зная тайну золотого сечения, умея его видеть в окружающих вещах, можно непосредственно выйти к Господу, возвратиться в духовное царство. В этом смысле 3 находится дальше от Единого (1), чем 2. Математически легче удалиться от 1, чем приближаться к этому числу. Вспомним теорию пределов:

Иначе, легче складывать и умножать, чем вычитать и делить (в математике при вычитании появляются новые числа — отрицательные, а при делении — дробные).

В эзотерическом смысле это понимается так, что приумножение богатства даётся легче и проще, чем сознательный отказ от ненужных наслоений материального мира. (Пример: с возрастом становится всё труднее что-то выбросить). Очень сложно, тем более, с кем-либо делиться тем, что имеешь (психологически). Но именно в этом и заключается духовный путь развития, мыслимый и объясняемый в терминах сакральной геометрии.

Золотое сечение — само число Ф присутствует в высшем творении Бога — в человеке. Так известные скульпторы и художники создавали свои наилучшие творения, применяя принцип золотого сечения. Из свойств числа Ф:

Ф=Ф²-1; Ф³=Ф²+Ф; Ф⁴=Ф³+Ф²,...

зная, что φ=1/Ф, легко составить второй ряд чисел:

1, φ, φ², φ³, φ⁴, ... которые и применяли скульпторы и художники.

Рассмотрим скульптуру Поликлета, которая получила название Канона (копьеносец или по-гречески Дорифор). Она создана скульптором около 440 лет до н.э. Её графический математический анализ такой: . Имея, эти отношения, легко просчитать идеальные (канонические отношения) для мужского тела.

Пропорции статуи

Поликлет, Дорифор (копьеносец)

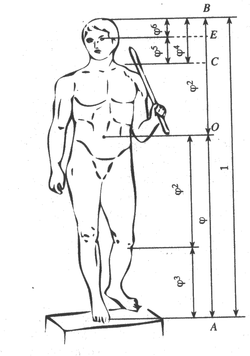
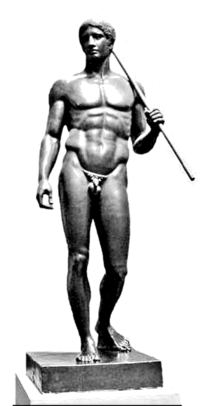
Иоган Кеплер именовал рассмотренное сечение божественным (Sectio diuina). Леонардо да Винчи назвал его золотым (Sectio anzza) — это название исторически и укрепилось.

Для гармонического соответствия должно быть всегда такое соотношение какое приведено на схеме с «Копьеносцем».

Рассмотрим второй пример: Венеру Боттичелли.

Пропорции Венеры Боттичелли

Боттичелли, Рождение Венеры

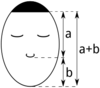
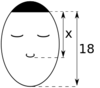
Можно рассмотреть любое лицо: измерить расстояние от линии волос на лбу до основания носа (a) и от основания носа до подбородка (b).

Если лицо идеально гармонично, то

Рассмотрим для примера лицо, где а=11 см и b=7 см, значит a+b=18 см. Подставим значения в формулу: . Видим, что соотношения приблизительно равны между собой и несколько отличаются от идеального соотношения 1,618. Вычислим идеальный вариант, отвечающий золотому сечению.

; ; ;

т. к. x > 0, то x ≈ -9+20,1 ≈ 11,1

т. е. a = 11,1 и b = 18-11,1 = 6,9

Дополним число Ф ещё несколькими свойствами:

1)

2) 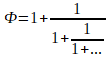– так называемая цепная дробь. Если обозначим эту дробь за х, то легко увидеть, что и в знаменателе первой дроби это же самое х, т. е. или x² – x – 1 = 0. Корень этого уравнения > 0 такой:

3) Из тригонометрии легко видеть: или .

Рассмотрим пример применение золотого сечения в строительных конструкциях. Знаменитый храм Парфенона:

Парфенон

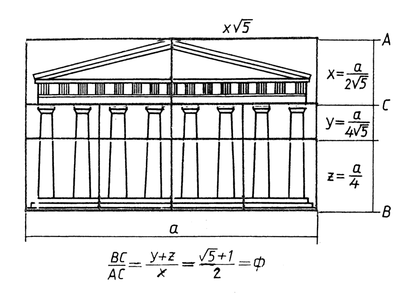
Рассмотрим 5-конечную звезду ABCDE, где AB=1, EH=JB=φ, HJ=φ²

Правильный пятиугольник с дважды вписанной пентаграммой

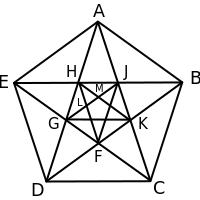
В пятиугольник HJKFG можно вписать следующий пятиугольник, в котором измерения составят:

GL=MJ=φ³, LM= φ⁴

И так далее. Все вписанные звёзды и 5-угольники имеют измерения: 1, φ, φ², φ³, φ⁴, φ⁵,...

В заключение можем сказать, что геометрическое знание уже изначально пребывает в нас, оно закладывалось в нас перед рождением, когда наши души пребывали в эфирных царствах (в иных планах бытия). На более высоких уровнях сознания мы естественным образом воспринимаем соразмерность Вселенной, на обыденном уровне в нашем распоряжении находятся духовные учения учителей Востока, изложенные в трудах Е.П.Б., её учеников и последователей; а также сакральная геометрия — как инструмент, помогающий обрести ощущения единства с Богом.

Источники:

1. Блаватская Е.П. Тайная Доктрина. Т. 1, 2.
2. Волошинов А.В. Математика и искусство. - М.: Просвещение, 1992, — 335 с.
3. Неаполитанский С.М. Сакральная геометрия / С.М. Неаполитанский, С.А. Матвеев - Спб.: Издательство института метафизики, 2006. — 632 с.

Сноски

---